En el siguiente artículo se muestro la distribución geométrica, su desarrollo, la varianza, esperanza, su función característica y su función generadora de momentos.
Esta distribución sirve para calcular la probabilidad de que ocurra un éxito por primera y única vez en el último ensayo que se realiza del experimento.
Función de densidad:
Sea A un suceso de probabilidad P(A)=p, y sea X la variable aleatoria que expresa el numero de fracasos que tiene lugar en las repeticiones independientes de pruebas de Benouili, hasta que ocurre A por primera vez. La variable X toma los valores de 0,1,2,….(numero de fracasos). Decimos que una variable aleatoria X sigue una distribución geométrica de parámetros p si su función de probabilidad es

dónde :
P= probabilidad de éxito en cada ensayo
x= ensayos que sean necesarios para obtener un éxito, para x = 1, 2, 3,..
Lo anterior solo se cumple si y solo si:
º Las pruebas son idénticas e independientes entre sí.
º La probabilidad de éxito es p y se mantiene constante de prueba en prueba
Función de distribución
La función de densidad de la variable aleatoria geométrica sólo depende del parámetro p, y presenta siempre una asimetría a la derecha como se puede observar en las siguientes funciones de densidad.
Función Generadora de Momentos
Demostración
Esperanza
Demostración
Varianza
Demostración
Por tanto
Función característica
La función característica se calcula teniendo en cuenta que de nuevo aparece la sumación de los términos de una progresión geométrica, pero esta vez de razón eit q:









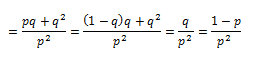

Su trabajo es bueno, no era tan necesaria la foto de perfil pero los temas se entienden, el tipo de letra esta bien.
ResponderEliminartienes un error en la definición de la función de distribución, la sumatoria debería empezar desde x = 1, además de que el término (1-p) debe estar elevado a la (x-1), como lo declaras al principio... este error se corre a lo largo de la función generatriz de momentos, faltaría multiplicar por el término e^t... saludos xD
ResponderEliminarMás bien mencionar que ese es un error es un error común en los principiantes y como acabas de mencionar, el recorrido es diferente, lo cual es la razón por la cual el coeficiente cambió. Esta es una forma alternativa de escribir la distribución de la geométrica.
ResponderEliminarPero (1-p) no puede estar nunca elevado a x, y tal y como figura en la fórmula se incluye este valor en el sumatorio... ¿no sería, tal y como está la fórmula, pero el sumario elevado a (x-1)?
ResponderEliminarMuy útil, tanto la teoría como las aplicaciones
ResponderEliminarHay dos formas de considerar la variable aleatoria Geométrica:
ResponderEliminar1) X = Número de ensayos en el que ocurre el primer éxito, en este caso los valores posibles de X son 1, 2, 3, ... (esta es la definición que ha usado)
2) Y = Número de fracasos antes de obtener el resultado considerado como éxito, en este caso los valores posibles de Y son 0, 1, 2, 3, ... . Claramente Y = X-1.
En la definición de la FD ha usado la segunda forma, también en la FGM. Por demás bien.